Kamis, 03 Oktober 2013

Fungsi Komposisi dan Fungsi Invers

Diposting oleh Unknown di 12.50

Fungsi/Pemetaan

Fungsi, atau disebut juga pemetaan, merupakan sebuah relasi yang khusus. Fungsi/pemetaan dari himpunan A ke himpunan B adalah relasi khusus yang memasangkan setiap anggota A, dengan tepat satu anggota B. Jadi, fungi sudah pasti sebuah relasi, tetapi relasi belum tentu sebuah fungsi.
Manakah yang merupakan fungsi?
Misalkan f adalah suatu fungsi yang memetakan x anggota A ke y anggota B, maka fungsi f dapat dinotasikan sebagai berikut:
f: x \rightarrow y atau f(x)=y
Jika x \in A , b \in B dan fungsi f  memetakan x ke y, maka y merupakan peta/bayangan dari x. Pada fungsi tersebut, himpunan A disebut daerah asal atau domain (Df), himpunan B disebut daerah kawan atau kodomain (Kf), sedangkan himpunan semua peta A di B disebut daerah hasil atau range (Rf).
Untuk jenis dan macam-macam fungsi sebenarnya ada banyak, misal fungsi konstan, fungsi identitas, fungsi linear, fungsi kuadrat, fungsi genap dan fungsi ganjil, fungsi modulus, maupun fungsi tangga. Mudah-mudahan bisa dibahas di lain kesempatan. Untuk postingan kali ini cukup membahas fungsi komposisi dan fungsi invers. Harap maklum

Fungsi Komposisi

Fungsi Aljabar
Sebelum ke fungsi komposisi, ada baiknya mempelajari terlebih dahulu fungsi aljabar. Apabila f dan g merupakan fungsi dari x, maka operasi aljabar yang dapat dilakukan adalah sebagai berikut:
  1. (f+g)(x)=f(x)+g(x)
  2. (f-g)(x)=f(x)-g(x)
  3. (f \times g)(x)=f(x) \times g(x)
  4. (\frac{f}{g})(x)=\frac{f(x)}{g(x)}
  5. f^n(x)=[f(x)]^n
contoh:
Diketahui f(x)=3x-1 ; g(x)=3-2x maka:
\begin{array}{rcl} (f+g)(x)&=&f(x)+g(x) \\ &=& (3x - 1) + (3 - 2x) \\ &=& x + 2 \end{array}
\begin{array}{rcl} (f-g)(x)&=&f(x)-g(x) \\ &=& (3x-1)-(3-2x) \\ &=& 5x -4 \end{array}
\begin{array}{rcl} (f \times g)(x)&=&f(x) \times g(x) \\ &=& (3x-1)(3-2x) \\ &=& -6x^2+8x-3 \end{array}
\begin{array}{rcl} (\frac{f}{g})(x)&=&\frac{f(x)}{g(x)} \\ &=& \frac{(3x-1)}{(3-2x)} \end{array}
Fungsi Komposisi
Misalkan f adalah suatu fungsi dari A ke B 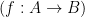(f:A \rightarrow B) dan g adalah fungsi dari B ke C (f:B \rightarrow C), maka suatu fungsi h dari A ke C (h: A \rightarrow C) disebut fungsi komposisi. Fungsi komposisi tersebut dinyatakan dengan h = g \circ f (dibaca: g bundaran f)
Fungsi Komposisi g bundaran f
Fungsi Komposisi: (f o g)(x) = f(g(x))
(f \circ g)(x) = f(g(x))
Fungsi Komposisi f bundaran g
Fungsi Komposisi: (g o f)(x) = g(f(x))
(g \circ f)(x) = g(f(x))
Sifat-sifat Komposisi Fungsi
1. Pada umumnya tidak komutatif
(g \circ f)(x) \neq (f \circ g)(x)
2. Operasi komposisi pada fungsi bersifat asosiatif
(f \circ (g \circ h))(x) = ((f \circ g) \circ h)(x)
3. Terdapat fungsi identitas I (x) = x
(f \circ I)(x) = (I \circ f)(x) = f(x)
 Contoh soal fungsi Komposisi:
Diketahui : fungsi f(x)=x-1 ; g(x) = x+2 ; h(x) = x^2-1 maka
\begin{array}{rcl}(f \circ g)(x) &=& f(g(x)) \\ &=& f(x+2) \\ &=& (x+2) -1 \\ (f \circ g)(x) &=& x+1\end{array}
\begin{array}{rcl}(g \circ f)(x) &=& g (f(x)) \\ &=& g(x-1) \\ &=& (x - 1) + 2 \\ (g \circ f)(x) &=& x-1\end{array}
\begin{array}{rcl}(g \circ h \circ f)(x) &=& g(h(f(x))) \\ &=& g(h(x-1)) \\ &=& g((x-1)^2 - 1) \\ &=& g(x^2 - 2x) \\ &=& (x^2 -2x) + 2 \\ (g \circ h \circ f)(x) &=& x^2 - 2x + 2 \end{array}
\begin{array}{rcl}(h \circ f \circ g)(x) &=& h(f(g(x)) \\ &=& h(f(x+2)) \\ &=& h((x+2)-1) \\ &=& h(x+1) \\ &=& (x+1)^2 - 1 \\ &=& (x^2 + 2x + 1)-1 \\ (h \circ f \circ g)(x) &=& x^2 + 2x\end{array}

Fungsi Invers

Apabila f adalah fungsi dari himpunan A ke himpunan B, maka invers fungsi f adalah suatu relasi dari himpunan B ke himpunan A. Jadi, invers suatu fungsi tidak selalu merupakan fungsi. Jika invers suatu fungsi merupakan fungsi, maka invers tersebut dinamakan fungsi invers dari fungsi semula.
Jika fungsi f: A \rightarrow B dinyatakan dengan himpunan pasangan berurutan f= \{ (x,y) | x \in A , y \in B\} maka invers fungsi f adalah f^{-1}: B \rightarrow A dan dinyatakan sebagai f^{-1}= \{ (x,y) | y \in B , x \in A\}
Fungsi f mempunyai fungsi invers f^{-1} jika dan hanya jika f merupakan fungsi (korespondensi satu-satu)
Langkah-langkah untuk menentukan rumus fungsi invers apabila fungsi f(x) telah diketahui:
  1. Mengubah persamaan y = f(x) dalam bentuk x sebagai fungsi y
  2. Bentuk x sebagai fungsi y tersebut dinamakan f^{-1}(y)
  3. Mengganti y pada f^{-1}(y) dengan x, sehingga diperoleh f^{-1}(x)
contoh:
Tentukan fungsi invers dari persamaan berikut:
f(x) = 3-2 dan f(x) = \frac{3x+4}{2x-1}
Jawab:
\begin{array}{rcl} f(x) &=& 3-2x \\ y &=& 3-2x \\ 2x &=& 3-y \\ x &=& \frac{3-y}{2} \\f^{-1}(y) &=& \frac{3-y}{2} \\ \therefore f^{-1}(x) &=& \frac{3-x}{2}\end{array}
\begin{array}{rcl} f(x) &=& \frac{3x+4}{2x-1} \\ y &=& \frac{3x+4}{2x-1} \\ y(2x-1) &=& (3x+4) \\ 2xy - y &=& 3x + 4 \\ 2xy - 3x &=& y+4 \\ x(2y-3) &=& y+4 \\ x &=& \frac{y + 4}{2y - 3} \\f^{-1}(y) &=& \frac{y+4}{2y-3} \\ \therefore f^{-1}(x) &=& \frac{x+4}{2x-3} \end{array}
Fungsi Ivers dari Fungsi Komposisi
Rumus untuk fungsi invers dari fungsi komposisi adalah sebagai berikut:
  • (f \circ g)^{-1} = g^{-1} \circ f^{-1}
  • (g \circ f)^{-1} = f^{-1} \circ g^{-1}
  • (f \circ g \circ h)^{-1} = h^{-1} \circ g^{-1} \circ f^{-1}
Demikian sedikit ulasan mengenai materi Fungsi Komposisi dan Fungsi Invers semoga bisa sedikit menambah wawasan kita. Untuk soal-soal latihannya akan ditambahkan di lain waktu. Jika berkenan, silakan berbagi dengan teman lain melalui tombol share di bawah. Kalau masih bingung dan ada yang ingin ditanyakan ditunggu di kolom komentar. Salam.

 

Label:

0 Comments:

Post a Comment



Subscribe to: Posting Komentar (Atom)

By :
Free Blog Templates